Persone e denaro
Ipotizziamo un esperimento sociale un poco assurdo: in una nazione lo stato ha distribuito a tutti i suoi cittadini la stessa quantità di denaro. Prima di questa distribuzione nessun cittadino possedeva denaro, dopo di essa cascuno cittadino si è ritrovato in tasca 1 Kinetic. A tutti i cittadini è vietato scambiare denaro con abitanti di altre nazioni, ma sono possibili scambi di denaro interni secondo uno schema ben preciso illustrato di seguito.
Ogni volta che due cittadini si incontrano, mettono in comune tutto il loro denaro e dividono il gruzzolo in due parti perfettamente a caso. Regolarmente avvengono moltissimi incontri e quindi scambi di denaro.
Traduciamo in formule questa operazione di suddivisione del denaro durante un incontro tra due persone. Definiamo le seguenti grandezze:
- \(e_1\) è il denaro posseduto dal primo cittadino prima dell'incontro;
- \(e_2\) è il denaro posseduto dal secondo cittadino prima dell'incontro;
- \(e_1'\) è il denaro posseduto dal primo cittadino dopo l'incontro;
- \(e_2'\) è il denaro posseduto dal secondo cittadino dopo l'incontro.
Visto che non si perde denaro è chiaro che \(e_1+e_2=e_1'+e_2'\). Queste due somme equivalgono all'ammontare del gruzzolo di cui sopra. Per dividerlo in due parti a caso sorteggiamo un numero reale \(x\) compreso tra 0 e 1. Il valore di \(x\) è sorteggiato da una opportuna distribuzione di probabilità \(p(x)\) decisa dal governo della nazione. Quindi possiamo affermare che le due persone dopo lo scambio si ritrovano in tasca rispettivamente:
- \(e_1'=x (e_1+e_2)\);
- \(e_2'=(1-x) (e_1+e_2)\)
Affinchè lo scambio di denaro sia in media equo, la distribuzione di probabilità \(p(x)\) deve essere simmetrica rispetto all'asse \(x=\frac{1}{2}\).
A questo punto la domanda è: come evolve la distribuzione della ricchezza dei cittadini di questa ipotetica e fantasiosa nazione?
Proviamo a rispondere simulando questa ipotetica economia al calcolatore, precisamente mediante un modello ad agenti. Scopriremo che la risposta alla domanda dipende dalla funzione \(p(x)\) introdotta sopra.
Prima di procedere facciamo ancora una riflessione sulla distribuzione di denaro nella nazione. Immediadamente dopo la distribuzione iniziale del denaro tutti i cittadini possiedono 1 Kinetic: questa situazione è estremamente ordinata. Esiste un solo modo possibile di realizzarla ed è quello in cui ogni persona possiede 1 Kinetic. Spiegamo meglio come contare i modi di realizzare una distribuzione di denaro con un secondo esempio un poco più disordinato del primo: tutti i cittadini possiedono 1 Kinetic tranne una persona che possiede 2 Kinetic. Se i cittadini sono \(N\) in totale, questa situazione è realizzabile in N modi perché ho \(N\) possibilità diverse di estrarre il cittadino fortunato con in tasca 2 Kinetic. Possiamo andare oltre e generalizzare questo calcolo, ma lasciamo quest'onere alla simulazione. È utile contare i modi in cui è possibile realizzare una determinata distribuzione di ricchezza? Si, perché consente di calcolare l'entropia della distribuzione: se \(W\) è il numero di modi di generare la distribuzione, l'entropia \(S\) vale:
\(S=k \log(W)\)
secondo la definizione statistica di entropia data da Boltzman. Porremo \(k = 1\) e tratteremo l'entropia come grandezza adimensionale.
La simulazione
“A simulation is the answer to the question, “What if…?”
Richard W. Hamming
Il codice della simulazione è disponibile sul mio repository Github. Consideriamo diverse distribuzioni di probabiltà \(p(x)\). Utilizziamo il parametro \(d\) intero (\(d\ge 2\)) per parametrizzare la famiglia di funzioni \(p(x)\) nel modo seguente:
\(p_d(x) = (x-x^2)^{\frac{d-2}{2}}\)
Torneremo sulla forma di queste funzioni più avanti. Ogni simulazione coinvolge 5000 persone e dura 20000 passi elementari: a ogni passo due cittadini a caso si incontrano, mettono sul tavolo tutto il denaro in loro possesso e se lo ridistribuiscono secondo le proporzioni \(x\) e \(1-x\). \(x\) è stato estratto a caso secondo la distribuzione di probabilità \(p_d(x)\). Su come estrarre un numero a caso secondo una distribuzione di probabilità data scriverò un articoletto prossimamente.
Vediamo che succede per i primi valori di \(d\). Il grafico seguente rappresenta la situazione per i 4 casi \(d=2, 3, 4, 5\) e riporta:
- la funzione \(p_d(x)\);
- la distribuzione della ricchezza dopo 20000 passi.
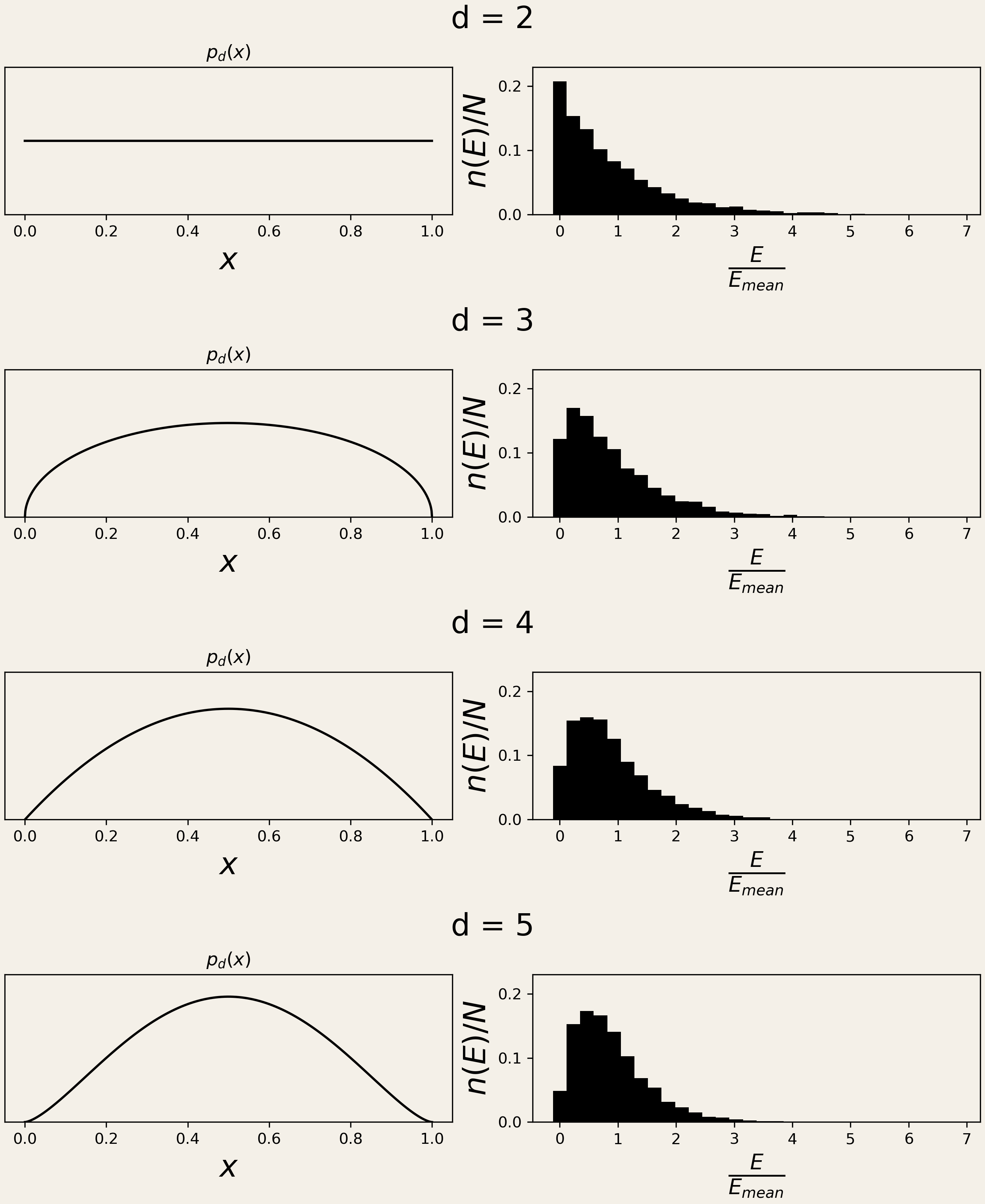
Nel caso \(d=2\) tutti i valori di \(x\) tra 0 e 1 sono equiprobabili e chi possiede poco o nulla costituisce la maggioranza della popolazione. All'aumentare di \(d\) la distrubuzione di probabilità \(p_d(x)\) tende a sfavorire sempre più gli scambi di denaro del tipo tutto o niente e di conseguenza i nullatenenti diminuiscono.
Ma cosa c'entra tutto questo con il secondo principio della termodinamica? Perché abbiamo scelto quella particolare forma analitica per la funzione \(p_d(x)\)? Risponderemo a queste domande nel prossimo articolo. Intanto ecco due video delle simulazioni per \(d=2\) e \(d=3\).
Caso \(d=2\)
Caso \(d=3\)
Riferimenti
Copyright 2023 by Simone Conradi and licensed under a
 Creative Commons Attribution 4.0 International License.
Creative Commons Attribution 4.0 International License.